⇒ Matury CKE
⇒ Rankingi
⇒ Wyniki uczniów
♦ Testy i arkusze
♦ Działy
♦ Rozwiązalność
⇒ Strona główna
⇒ Zaloguj mnie
Siatki graniastosłupów. Pole powierzchni graniastosłupa
Zadania dla klasy trzeciej liceum ogólnokształcącego - poziom podstawowy
- geometria przestrzenna
- graniastosłupy
- siatki graniastosłupów
- pole powierzchni graniastosłupa
| Zadanie 1. 2 pkt ⋅ Numer: pp-20802 ⋅ Poprawnie: 70/264 [26%] | Rozwiąż |
Podpunkt 1.1 (2 pkt)
Wysokość graniastosłupa prawidłowego czworokątnego jest równa
h, a jego przekątna tworzy z płaszczyzną podstawy
kąt o mierze \alpha.
Oblicz pole powierzchni całkowitej tego graniastosłupa.
Dane
h=20
\cos\alpha=\frac{9}{41}=0.21951219512195
\cos\alpha=\frac{9}{41}=0.21951219512195
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 2. 4 pkt ⋅ Numer: pp-30281 ⋅ Poprawnie: 25/34 [73%] | Rozwiąż |
Podpunkt 2.1 (4 pkt)
« Mały Jaś bawi się klockami w kształcie sześcianu o boku długości
2. Ze wszystkich klocków zbudował sześcian o krawędzi
8, który następnie zburzył i z klocków
utworzył graniastosłup prawidłowy czworokatny. Wówczas okazało się, że został
mu jeden klocek. Oblicz pola powierzchni całkowitych obu brył.
Podaj stosunek tych pól należący do przedziału (0,1).
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 3. 4 pkt ⋅ Numer: pp-30374 ⋅ Poprawnie: 2/7 [28%] | Rozwiąż |
Podpunkt 3.1 (2 pkt)
« W graniastosłupie ABCA'B'C' krawędzie podstawy
AB i BC przecinają się
pod kątem o mierze 120^{\circ},
a trójkąt A'BC' jest równoboczny.
Oblicz długość krawędzi podstawy AC.
Dane
|AB|=6\sqrt{6}=14.69693845669907
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 3.2 (2 pkt)
Oblicz pole powierzchni całkowitej tego graniastosłupa.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 4. 4 pkt ⋅ Numer: pp-30378 ⋅ Poprawnie: 17/77 [22%] | Rozwiąż |
Podpunkt 4.1 (2 pkt)
« Podstawą graniastosłupa prostego ABCDA'B'C'D' jest romb
ABCD, którego przekątna AC'
tworzy z płaszczyzną podstawy kąt o mierze \alpha,
a przekątna BD' tworzy z tą samą podstawą kąt
o mierze \beta.
Oblicz pole powierzchni podstawy tego graniastosłupa.
Dane
|AC'|=16
\alpha=45^{\circ}
\beta=30^{\circ}
\alpha=45^{\circ}
\beta=30^{\circ}
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 4.2 (2 pkt)
Oblicz pole powierzchni bocznej tego graniastosłupa.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 5. 4 pkt ⋅ Numer: pp-30321 ⋅ Poprawnie: 27/109 [24%] | Rozwiąż |
Podpunkt 5.1 (2 pkt)
Wysokość czworościanu foremnego ma długość H.
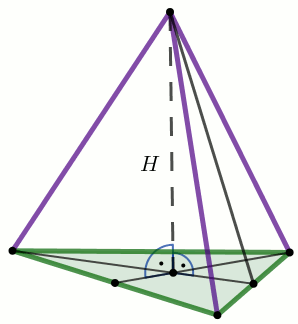
Oblicz długość krawędzi podstawy tego czworościanu.
Dane
H=\frac{11\sqrt{3}}{2}=9.52627944162883
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 5.2 (2 pkt)
Oblicz pole powierzchni całkowitej tego czworościanu.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 6. 4 pkt ⋅ Numer: pp-30386 ⋅ Poprawnie: 7/72 [9%] | Rozwiąż |
Podpunkt 6.1 (2 pkt)
« Suma wszystkich krawędzi ostrosłupa prawidłowego trójkątnego
ABCS o podstawie ABC
jest równa d:
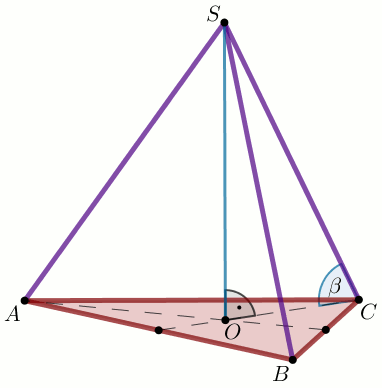
Oblicz długość krawędzi jego podstawy.
Dane
d=336
\cos\beta=\frac{\sqrt{3}}{18}=0.09622504486494
\cos\beta=\frac{\sqrt{3}}{18}=0.09622504486494
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 6.2 (1 pkt)
Oblicz wysokość tego ostrosłupa.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 6.3 (1 pkt)
Oblicz pole powierzchni bocznej tego ostrosłupa.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)