Walec
Zadania dla liceum ogólnokształcącego - poziom podstawowy
- bryły obrotowe
- walec
| Zadanie 1. 1 pkt ⋅ Numer: pp-11440 ⋅ Poprawnie: 36/81 [44%] | Rozwiąż |
Podpunkt 1.1 (1 pkt)
Na walcu umieszczono półkulę o promieniu równym promieniowi walca i wysokości
2 razy większej od promienia półkuli:
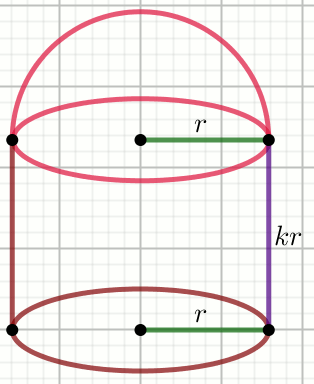
Objętość tej bryły jest równa p\cdot r^3\pi.
Podaj liczbę p.
Odpowiedź:
| p= | |
| Zadanie 2. 1 pkt ⋅ Numer: pp-11381 ⋅ Poprawnie: 17/35 [48%] | Rozwiąż |
Podpunkt 2.1 (1 pkt)
Przekrojem osiowym walca jest kwadrat o polu powierzchni
\frac{7}{2}\pi.
Zapisz pole powierzchni bocznej tego walca w postaci p\cdot \pi^{k}
gdzie p\in\mathbb{W} i k\in\mathbb{N}.
Podaj liczby p i k.
Odpowiedzi:
| p | = |
(wpisz liczbę zapisaną dziesiętnie) |
| k | = |
(wpisz liczbę zapisaną dziesiętnie) |
| Zadanie 3. 1 pkt ⋅ Numer: pp-11382 ⋅ Poprawnie: 172/269 [63%] | Rozwiąż |
Podpunkt 3.1 (1 pkt)
« Walec ma przekrój osiowy, który jest kwadratem. Jego pole
powierzchni bocznej jest równe 16\pi.
Objętość tego walca jest równa p\cdot \pi.
Podaj liczbę p.
Odpowiedź:
p=
(wpisz liczbę całkowitą)
| Zadanie 4. 1 pkt ⋅ Numer: pp-12438 ⋅ Poprawnie: 224/257 [87%] | Rozwiąż |
Podpunkt 4.1 (1 pkt)
Objętość walca o promieniu podstawy 2 jest równa
4\sqrt{11}\pi^2.
Wysokość h tego walca jest równa:
Odpowiedzi:
| A. \sqrt{11}\pi | B. \frac{\sqrt{11}}{2}\pi |
| C. 22 | D. 2\sqrt{11} |
| E. \frac{\sqrt{11}}{4} | F. 3\sqrt{11}\pi |
| Zadanie 5. 1 pkt ⋅ Numer: pp-12457 ⋅ Poprawnie: 64/160 [40%] | Rozwiąż |
Podpunkt 5.1 (1 pkt)
Pole powierzchni całkowitej walca \mathcal{F}_1 jest równe
22\pi, a objętość tego walca jest równa
10\pi. Walec \mathcal{F}_2
jest podobny do walca \mathcal{F}_1 w skali k=2.
Oceń prawdziwość poniższych zdań.
Odpowiedzi:
| T/N : pole powierzchni całkowitej walca \mathcal{F}_2 jest równe 44\pi | T/N : objętość walca \mathcal{F}_2 jest równe 40\pi |
| Zadanie 6. 2 pkt ⋅ Numer: pp-20697 ⋅ Poprawnie: 10/45 [22%] | Rozwiąż |
Podpunkt 6.1 (2 pkt)
Pole powierzchni całkowitej walca wynosi 48\pi i jest
o 12\pi większe od pola powierzchni bocznej tego
walca.
Oblicz objętość tego walca.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 7. 4 pkt ⋅ Numer: pp-30293 ⋅ Poprawnie: 14/45 [31%] | Rozwiąż |
Podpunkt 7.1 (4 pkt)
« Pobocznica walca jest prostokątem o przekątnej długości
8, która tworzy kąt \alpha
z bokiem odpowiadającym wysokości.
Oblicz objętość tego walca wiedząc, że \cos\alpha=\frac{1}{4}.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)